LeetCode 刷题基础 -- 模板原型Ⅰ

学习网站

晴问算法训练营

一、进制转换

十进制数 n 转 q 进制

    int n,a[1000],len=0;
    cin>>n;
    do{
   
        a[len++] = n % q;
        n /= q;
    }while(n>0);
    for(int i= len-1;i>=0;i--){
   
        cout<<a[i];
    }

p进制数 n 转 Q进制

int y = 0,product = 1;   //product 不断乘以p
while( n != 0){
   
    y += (n%10) * product;
    n /= 10;
    product *= p
}

二、二分查找

① 查找指定元素

//  查找指定元素
int findX(int a[],int l,int r,int x){
   
    int mid;
    while( l<= r){
      //注意<= 号
        mid = (l + r) / 2;
        if(a[mid]==x){
   
            return mid;
        }else if(a[mid] < x){
   
            l = mid + 1;
        }else{
   
            r = mid - 1;
        }
    }
    return -1;
}
int main(){
   
    cout<<findX(a,0,n-1,x); //n为数组长度
}

② 查找第一个大于等于 x 值的序列下标

// 查找第一个大于等于 x 值的序列下标
int findX(int a[],int l,int r,int x){
   
    int mid;
    while(l < r){
      // 注意< 号
        mid = (l+r)/2;
        if(a[mid] >= x){
     //
            r = mid;
        }else{
   
            l = mid + 1;
        }
    }
    return l;  // 注意return l
}

③ 查找第一个大于 x 值的序列下标

int findX(int a[],int l,int r,int x){
   
    int mid;
    while(l<=r){
   
        mid = (l+r)/2;
        if(a[mid]<=x){
   
            l = mid + 1;
        }else{
   
            r = mid - 1;
        }
    }
    return l;
}

④ 单峰序列

单峰序列是指，在这个序列中存在一个位置，满足这个位置的左侧（含该位置）是严格递增的、右侧（含该位置）是严格递减的，这个位置被称作峰顶位置。现在给定一个单峰序列，求峰顶位置的下标。

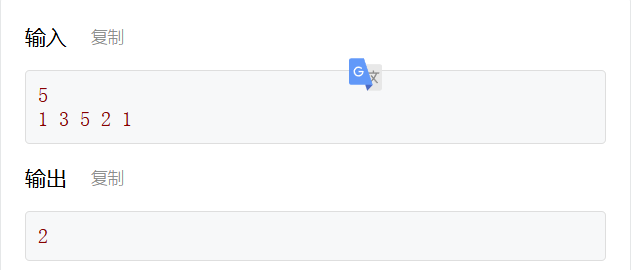
int maxIn = 0;
int mx = 0;
void findX(int a[],int l,int r){
   
    if(l>r)
        return ;
    int mid = (l+r)/2;
    if(a[mid]>mx){
   
        mx = a[mid];
        maxIn = mid;
    }
    findX(a,mid+1,r);
    findX(a,l,mid-1);
}

三、双指针

① 两数之和

给定一个严格递增序列A和一个正整数k，在序列A中寻找不同的下标i、j，使得Ai+Aj=k。问有多少对(i,j)同时i<j满足条件。

int i=0,j=n-1,cnt=0;
    while(i<j){
   
        if(a[i]+a[j]==k){
   
            cnt++;
            i++;
            j--;
        }else if(a[i]+a[j]<k){
   
            i++;
        }else{
   
            j--;
        }
    }

② 序列合并

给定两个升序的正整数序列A和B，将它们合并成一个新的升序序列并输出。

int merge() {
   
    int i = 0, j = 0, counter = 0;
    while (i < n && j < m) {
   
        if (a[i] < b[j]) {
   
            mergedNums[counter++] = a[i++];
        } else {
   
            mergedNums[counter++] = b[j++];
        }
    }
    while (i < n) {
   
        mergedNums[counter++] = a[i++];
    }
    while (j < m) {
   
        mergedNums[counter++] = b[j++];
    }
    return counter;
}

③ 集合求交

给定一个包含 n 个正整数的集合 S1，再给定一个包含 m 个正整数的集合 S2，求两个集合的交集。

void getIntersection() {
   
    int i = 0, j = 0;
    while (i < n && j < m) {
   
        if (a[i] == b[j]) {
   
            intersection.push_back(a[i]);
            i++, j++;
        } else if (a[i] < b[j]) {
   
            i++;
        } else {
   
            j++;
        }
    }
}

④ 集合求并

给定一个包含 n 个正整数的集合S1，再给定一个包含 m 个正整数的集合S2，求两个集合的并集。

void getUnionSet() {
   
    int i = 0, j = 0;
    while (i < n && j < m) {
   
        if (a[i] == b[j]) {
   
            unionSet.push_back(a[i]);
            i++, j++;
        } else if (a[i] < b[j]) {
   
            unionSet.push_back(a[i++]);
        } else {
   
            unionSet.push_back(b[j++]);
        }
    }
    while (i < n) {
   
        unionSet.push_back(a[i++]);
    }
    while (j < m) {
   
        unionSet.push_back(b[j++]);
    }
}

四、其他高效技巧与算法

① 区间和

给定由n个正整数组成的序列A，接下来给出k个查询，每个查询指定两个正整数l、r，计算序列从第l个整数至第r个整数之和，即Al+Al+1+…+Ar。

int main() {
   
    int n;
    cin >> n;
    vector<int> A(n + 1);
    vector<int> prefixSum(n + 1, 0);
    
    // 读取原数组并构建前缀和数组
    for (int i = 1; i <= n; ++i) {
   
        cin >> A[i];
        prefixSum[i] = prefixSum[i - 1] + A[i];
    }
    
    int k;
    cin >> k;
    for (int i = 0; i < k; ++i) {
   
        int l, r;
        cin >> l >> r;
        // 计算区间和并输出结果
        cout << prefixSum[r] - prefixSum[l - 1]